이 글은 반도체칩의 제조공정, 특히 Device가 세밀화되는 시점인 EUV(극자외선)공정이 진행되면서 반도체 공정, 특히 Lithography에 기인한 패터닝공정과 연관된 글이다. Stochastics와 연관된 Rougness는 Device에 많은 문제를 야기 시키며, 이런 문제들의 요인은 아래와 같은 문제로 정리할수 있다.
- Within-Feature roughness의 문제, 즉 선폭의 Roughness, LWR, LER이 해당이 되며, 이것들은 전기적인 특성에 영향을 준다.
- Feature와Feature의 오차를 만드는 문제, 즉 LCDU(Local CD Uniformity),LPPE(Local Pattern Placement errors),LEPE(Local Edge Placement Error)등이 해당된다. (이 용어들은 반도체공정중 특히 Etch,Photo의 패터닝의 전문용어임).
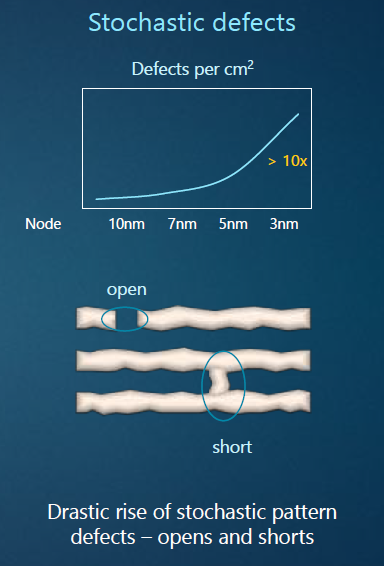
- 웨이퍼 패터닝시 생기는 큰 문제들, 즉 Bridge,Short, Missing Contacs등이 해당이 된다. 이 문제들은 바로 Chip의 성능에 문제가 생기게 하는 Major Defects이다.
- 궁극적으로 위의 나열된 문제들이 Device Yield와 Performance를 낮게 만드는 요인이다.
예를 들어 Line & Spacer의 분석(LER,LWR등의) Long Line분석을 통해 유용한 정보를 획득할수 있으며, 이 정보를 활용하여 Stochastic Behavior에 대해 해석과 분석을 할수 있다.
위에 열거한 용어들의 정의를 정리해 보자

LER은 Y의 평평한 기준선을 중심으로 표준편차(3Sigma)를 구한 값이다. 즉 Line에 얼마나 거칠기의 정도인지를 정의한다.

LER은 위의 그림과 같이 단지 하나의 Line의 딱 Edge Roughness만을 대변할 뿐이다. Line의 편차만을 나타낸다.위의 4가지 Line을 본다면 Line의 Roughness는 모두 다르다고 생각을 당연히 할것이다.그러나 LER를 Value로 표시를 한다면 단순히 표준편차의 숫자로 비슷한 Value가 나올수 있다.따라서 LER은 다른 방식으로 이 형상들을 표현(Characterizing)하는것을 만들어야 한다.
그렇다면 Line의 길이에 따른 Roughness의 해석 Model은 아래의 3가지가 대표적이다.

ACF,HHCF,PSD는 모두 함수로 상호 연결이 되어 있다. 그러나 3개의 함수는 실직적으로 보면 응용하는 방법에 따라 다른 약간의 차이점이 있다. ACF나 HHCF에 대한 개념은 나중에 다루도록 하자.
이들중에 반도체 공정에서 널리 사용되는 SEM측정의 해석에는 PSD(Power Spectral Density)가 가장 적절하고 실용적인 방법이고 이것에 대한 추가 설명을 하겠다.
PSD는 Roughness를 Frequency domain함수를 근거로 산출한다. PSD는 Fourier Transform(푸리에변환)의 식을 Edge roughness와 Frequency함수로 정의를 하는것이다.

복잡해 보이는 식은 이정도까지만 이해를 하고... 실제적으로 나타나는 PSD Curve의 예를 보자.

Frequency(1/f)는 위와 같이 도식화가 되는데, 즉 Frequency는 간단히 일정선폭에서 얼마나 진동(Noise)또는 Roughness가 존재하는지를 나타내는 값이다. 물론 전파나, 파동처럼 일정하고 주기적인 Frequency는 아니다(위의 그림처럼)
그러나 Line roughness를 해석하는 방법중 이 Frequency를 하나의 인자로 적용을 한다.
위의 그림에서 우측 X축으로 본다면 High Frequency(HF)는 Line의 짧은 길이를 대변하며 Low Frequency(LF)는 긴Line을 대변할수 있다. 일정한 선폭안의 진동수를 Roughness(거칠기)로 해석을 한다는 개념이다.
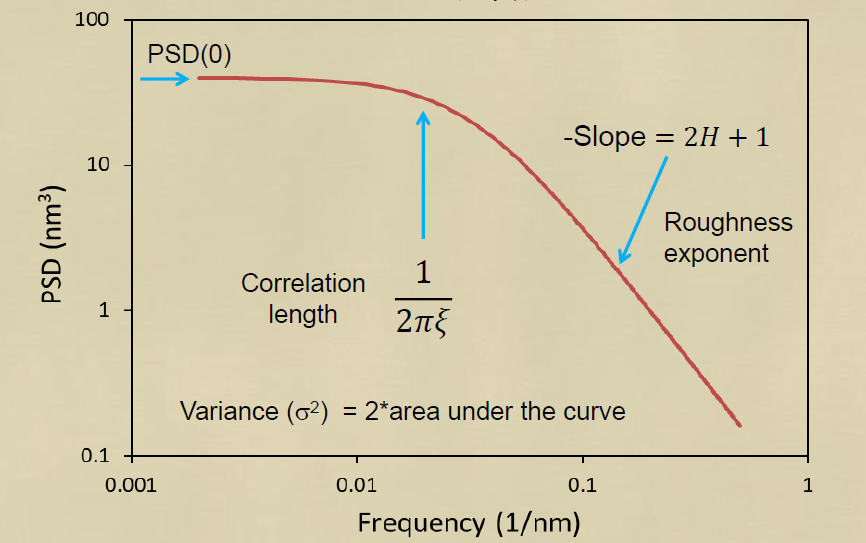
이 방법은 널리 알려진 가장 일반적인 PSD의 표현방법이며, PSD의 거동을 설명하는 기본적인 인자이다.
PSD의 일반적인 거동은 위와 같이 LF영역에서는 Flat한 PSD가 HF영역으로 가면서 급격이 아래로 Slope이 지게 된다.이 거동은 예외적인 경우를 제외하고는 우리가 측정하는 가장 일반적인 LER를 볼때의 형태라 할수 있다.
PSD의 이론은 위에서 언급했듯이 ACF와 연결된 푸리에변환식의 한쌍이다.
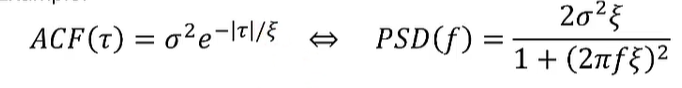
위의 PSD Graph의 Low Frequency영역의 Flat한 부분은 White Noise의 이상적인 결과다.
White Noise란 의미는 독립적으로 생기는 인자들 즉. Uncorrelated or Independent randomness이다. Photon의 Shot noise, Photon Absorption, Chemical의 농도, Acid의 생성등이 해당이 된다.
위의 말을 이해하려면, Lithography영역의 불확실성을 만드는 인자들을 이해를 해야 하는데...
아래 그림을 보자..
포토공정에서 레지스트위의 패터닝을 형성하는 과정에는 일정공간안의 아래의 인자들이 Random하게 일어난다.
-포톤의 갯수
-PAG의 위치 : PAG는 Resist의 주요성분..
-빛과 반응해서 생성되는 산(Acid)와 흡수도-빛과 Resist가 반응할때의 폴리머의 결합길이-Blocking Position은 패턴에 의해 Photon이 가지 못하고 가려지는 인자들.화학적 반응확산정도
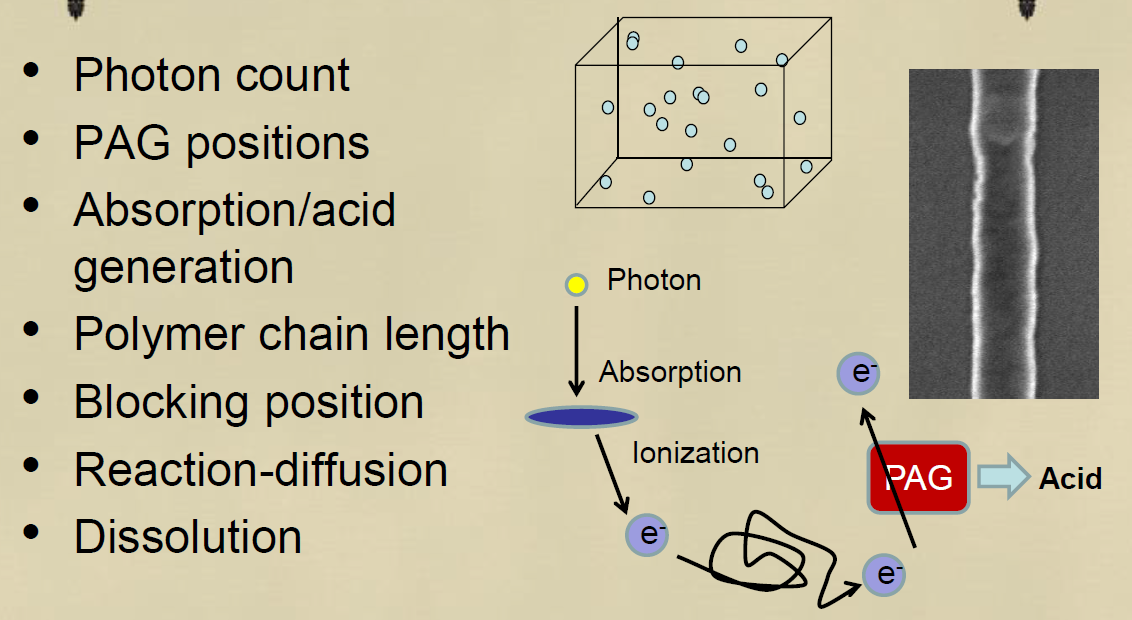
따라서 그래프의 거동인자를 해석을 하면 원하는 Line roughness의 원인이 되는 거동을 이론적으로 추측하고 계산이 가능하다.
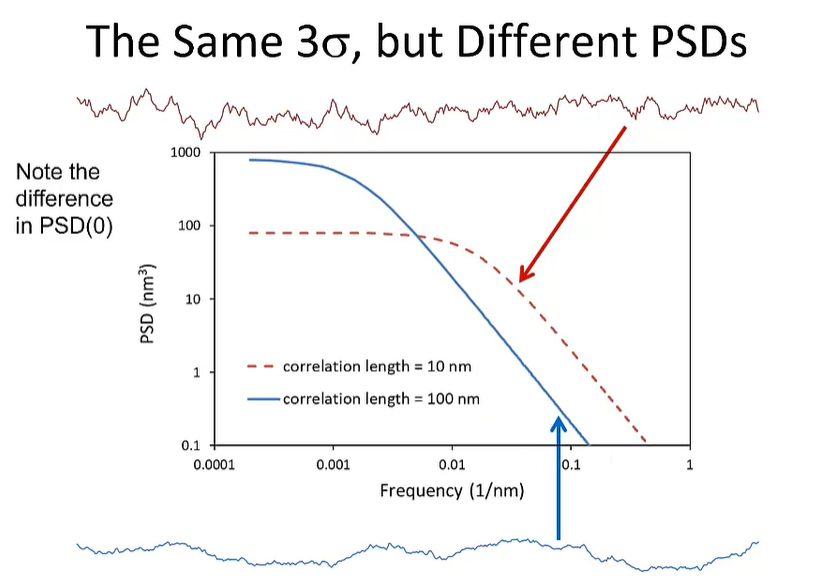
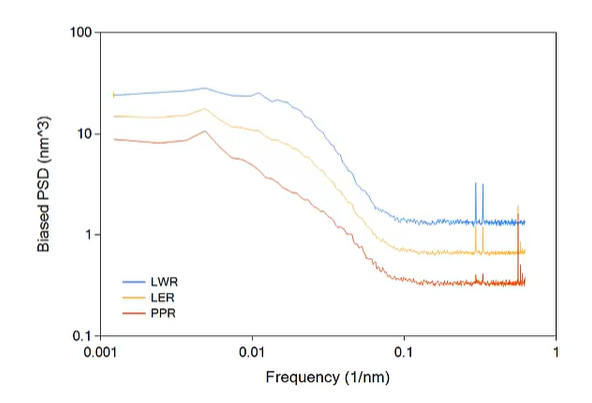
그러면 같은 LER 3Sigma의 다른 PSD의 거동을 아래에 보자Red Line의 경우는 Low Frequency에서 rougness가 크고, Blue의 경우는 High Frequency에서 Roughness level이 크다. 이런 차이가 나는 이유는 Correlation Length의 차이와 PSD(0)의 차이 때문이다.
따라서 이 두개의 다른 거동의 Graph가 실제 Device의 패터닝에 기인하여 큰 영향의 차이를 만든다.실제 LER로 보면 차이가 없지만..... PSD의 차이가 난다는 이야기.
위에는 이상적인 PSD의 이론을 개략적으로 이해를 했다.
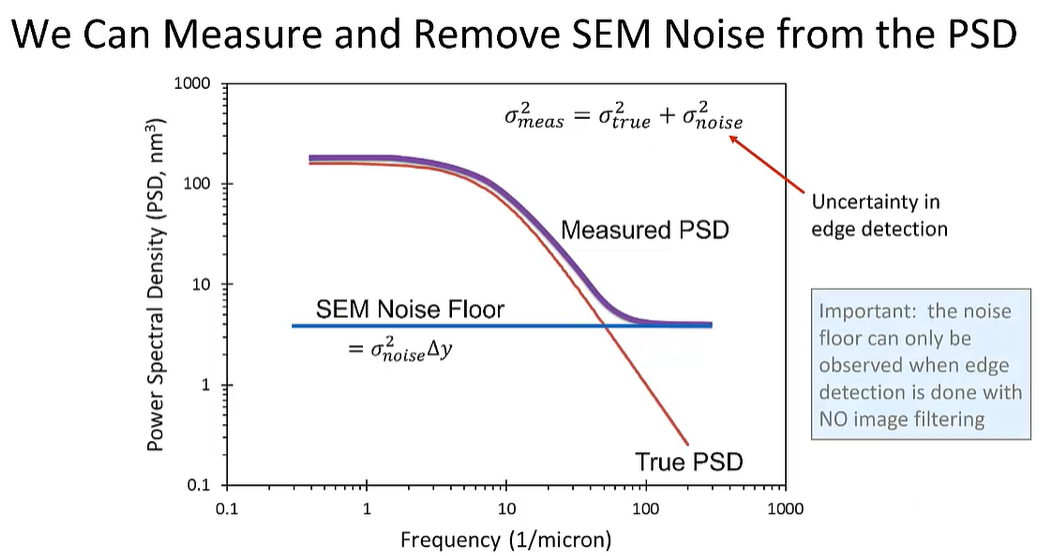
아래는 실제 SEM Tool에서 측정한 Data는 아래와 같이 PSD의 불확실성보다 더 지배적인 인자들이 Noise로 나타난다.
예를 들어 측정장비에 기인한 Noise, 그리고 주변인자들에게 기인하는 Aliasing Noise등으로 실제 PSD Graph는 이 Noise를 포함하여 아래와 같이 Graph가 나타나진다.. 이를 Noise Floor라 부르자.

그렇다면 이 Noise Floor를 통해 Noise 즉 True Noise를 추출할수가 있다
아래의 추출한 Noise Floor는 보이는바와 같이 고유의 Noise가 존재하고 이 Noise를 빼면 하면
진짜 True PSD, 즉 Unbiased PSD의 계산이 가능해진다.
정리를 해보자.모든 SEM장비의 Noise는 White Noise로 아래와 같이 Flat한 거동을 한다. 이 Noise는 모두 Edge Detection이 발생되는 Noise이며 여기에 이상적인 True PSD를 대입하여 실제 측정된 PSD값을 산출할수 있다.중요한것은 Noise Floor의 SEM측정은 반드시 Image filtering이 없는 Pure Noise가 필요하다.
자 실제적으로 SEM의 측정 Frame(Shot의 수)에 따른 Noise Level의 예를 보자(아래)
Frame에 따라 Noise가 많이 보이며, 당연히 Noise Floor에 근사한 Graph경향성을 보인다.
Frame수가 증가함에 따라 Noise Level이 줄어든다.

위에서 설명했던 Unbiased PSD를 여기서 추출을 하면 아래와 같이 된다.

따라서 우리는 Unbiased PSD를 추출을 하면 SEM Image의 Noise Level에 따란 불확실성을 제거하고
신뢰성이 있는 실제 Line roughness의 측정이 가능하다.
마지막으로 반도체 공정의 집적화는 EUV공정과 함께 10나노부터 7나노..앞으로 5나노까지 도전을 하고 있으며 여기의 공정의 핵심은 줄어든 선폭만큼 Roughness를 얼마만큼 잘 Control하고 Stochastic Issue를 해결하는 도전이다.
선폭의 줄어든 만큼, 이전의 Technode에서 도전받지 못했던 많은 문제들중의 하나가 Roughness문제인것이다.


'반도체' 카테고리의 다른 글
| ASML은 왜 Berliner Glas라는 독일회사를 인수를 했을까? (0) | 2022.03.22 |
|---|---|
| 중국 반도체 장비회사의 현황 (0) | 2021.12.28 |
| 반도체공정 웨이퍼 패터닝 기법 (0) | 2021.08.19 |
| 반도체 공정 OPC(Optical Proximity Correction)의 이해 (1) | 2021.08.19 |
| RF Filter 시장 분석 및 Market Players (0) | 2021.08.13 |